Outline
Resonant x-ray diffraction (RXD), different from the conventional x-ray diffraction, is performed at the specific wave length or energy. It is mostly at the absorption edge of the resonant atom. It provides us unique information of the ordered system like spin, orbital, and charge, which cannot be observed by the conventional x-ray diffraction. Most important feature of RXD is the dependency on the x-ray polarization, that discloses the presence of multipole’s order such as electric quadruple order in CeB\(_6\), magnetic octupole order in Ce\(_{0.7}\)La\(_{0.3}\)B\(_6\), hexadecapole order DyB\(_2\)C\(_2\). In addition, circular polarized x-rays identify the handedness of a crystal and magnetic chirality. The optical activity is another tool to observe the handedness, however, it is not necessarily to identify it.
Atomic Form factor
The atomic form factor \(f\) , or the atomic scattering length represents the scattering amplitude for the x-ray. The diffraction intensity is proportional to the square of the unit-cell structure factor \(F\), which is given by a sum of the atomic form factors \(f_i\) of ions in a unit cell with their phase factors,
\[ F=\sum_{i}f_i \exp(i \mathbf{Q} \cdot \mathbf{r}_i). \]
Here \(\mathbf{Q}=\mathbf{q}_i-\mathbf{q}_f\) is the momentum transfer for the diffraction, with the initial and the diffracted x-ray momentum, \(\mathbf{q}_i\) and \(\mathbf{q}_f\). The atomic form factor \(f\) consists of non-dispersive term \( f_0\) and dispersion correction terms \( f’ + i f^{\prime\prime}\) with energy,
\begin{equation}
f= f_0 + f^{\prime} + i f^{\prime\prime}.\tag{1}
\end{equation}
The term \(f_0\) comes from the \( \mathbf{A}^2\) term in the Hamiltonian, and the terms \( f’ + i f^{\prime\prime}\) come from the \( \mathbf{A} \cdot \mathbf{p} \) term in the Hamiltonian (See the next page).
One finds
\begin{equation}
f= f_0 + f^{\prime} + i f^{\prime\prime} + f^{mag}_{non-res.} \tag{2}
\end{equation}
in the literature [1,2]. There are two non-resonant magnetic scattering terms in \(f^{mag}_{non-res.}\). One, which has certain polarization dependence, is given by M. Blume [3]. This term is deduced from the \(\mathbf{A} \cdot \mathbf{p}\) and the \(\boldsymbol{\sigma} \cdot \mathbf{B}\) terms in the limit where \(\hbar \omega \) is far from the absorption edge. The other is deduced from \(\boldsymbol{\sigma} \cdot \mathbf{E} \times \mathbf{A}\) term. This term is not related with the resonance and its polarization dependence is the same as the charge scattering. The term \(\boldsymbol{\sigma} \cdot \mathbf{B}\) appears in magnetic dipole (\(M\)1) transition at the resonance. However, it is too small to detect it.
Absorption edge
The absorption edges of the atom appear at the energy of the core electron state depending on its quantum numbers, n, l, m. For example, Si K edge is at E=1852 eV.
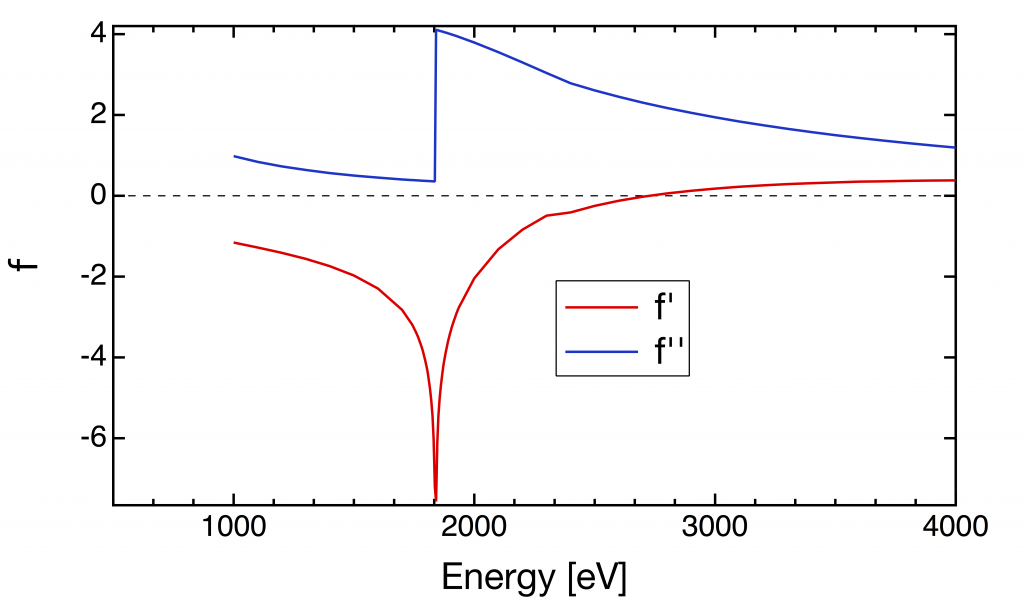
Figure 1: The scattering form factor of Si; energy dispersion.
Figure 1 shows the atomic form factor of Si as a function of the X-ray energy.
Bragg Law
\[ 2d \sin \theta = \lambda \]
\[ Q=\frac{4\pi \sin \theta}{\lambda}\ = \frac{2\pi}{d} \]
References
[1] J.P. Hannon et al., Phys. Rev. Lett. 61 1245 (1988).
[2] J.P. Hill and D.F. McMorrow, Acta Crystallogr. Sec.A 52, 236 (1996).
